
知乎问题链接:如何用C++10行内写出八皇后
前日闲暇之余乱逛,看到了这个问题,觉得蛮有意思。
也顺便想改进一下通行的官方解法,就认真写了一下,
顺便也把自己作为外行人的一点感想列在下面。
n皇后问题,较早为八皇后问题,出现于1848年。
Max Bezzel讨论的是“在国际象棋上出现8个后时,
应该如何排列,才可使她们不会相爱相杀。”
 (八皇后问题的其中一个解)
(八皇后问题的其中一个解)
虽然依照升变原则,同棋盘上可以出现17个后,
(一方全升变,一方被吃过路兵一次,加上初始两个)
但是真正走出来的可能性是微乎其微的。
况且这个问题没有考虑黑白方关系,
在象棋上也就是趣味的一问而已。
——直到图论和函数式编程思想出现,
穷举法和递归思想使得92个解终于呼之即出。
前面说到,n皇后问题的解法都是穷举法及递归,
加上回溯算法实现。这对于刚入门的傻喵来讲,
是很好的练习题目了——
' n queens cast by go basic
[loop]
input "How many queens (N>=4)";n
if n < 4 then
print "Must be greater than 4"
goto [loop]
end if
dim plot$(100,100)
dim q(n+20)
dim e(n+20)
dim o(n+20)
r=n mod 6
if r<>2 and r<>3 then
gosub [samp]
goto [shoBoard]
end if
for i=1 to int(n/2)
e(i) = 2 * i
next
for i=1 to int((n/2)+.5)
o(i) = 2 *i-1
next
if r = 2 then gosub [edt2]
if r = 3 then gosub [edt3]
s = 1
for i=1 to n
if e(i)>0 then
q(s) = e(i)
s = s+1
end if
next
for i=1 to n
if o(i) > 0 then
q(s) = o(i)
s = s + 1
end if
next
' print board
[shoBoard]
cls
for i = 1 to n
plot$(i,26-q(i)) = "*"
plot$(i,24-n) = chr$(96+i)
plot$(n+1,26-i) = str$(i)
next i
for ii = 1 to 100
for jj = 1 to 100
print left$(plot$(jj,ii)+" ",1);
next jj
print
next ii
end
' the simple case
[samp]
p = 1
for i = 1 to n
if i mod 2=0 then
q(p) = i
p = p + 1
end if
next i
for i = 1 to n
if i mod 2 then
q(p) = i
p = p + 1
end if
next
return
' edit list when remainder is 2
[edt2]
for i=1 to n
if o(i) = 3 then
o(i) = 1
else
if o(i)=1 then o(i) = 3
end if
if o(i) = 5 then
o(i)= o(i) -1
else
if o(i) = 0 then
o(i) = 5
return
end if
end if
next
' edit list when remainder is 3
[edt3]
for i = 1 to n
if e(i) = 2 then
e(i) = e(i)-1
else
if e(i) = 0 then
e(i) = 2
goto [more]
end if
end if
next i
' edit list some more
[more]
for i = 1 to n
if (o(i)=1 or o(i)=3) then
o(i) = o(i)-1
else
if o(i) = 0 then
o(i) = 1
o(i+1) = 3
return
end if
end if
next
或是这样的尝试——
# Brute force permutations for 8 queens by R
safe <- function(p) {
n <- length(p)
for (i in seq(1, n - 1)) {
for (j in seq(i + 1, n)) {
if (abs(p[j] - p[i]) == abs(j - i)) return(F)
}
}
return(T)
}
queens <- function(n) {
p <- 1:n
k <- 0
while (!is.null(p)) {
if(safe(p)) {
cat(p, "\n")
k <- k + 1
}
p <- next.perm(p)
}
return(k)
}
queens(8)
在好多人的口中,递归+穷举已然成为了8皇后问题的标准答案。
但是时代还是会变的,人的能力也是在随着问题进步的。
当面临N皇后问题时,传统的方法则捉襟见肘。
虽然有人推荐直接向上抽象,利用已有的库来简化方法,
但是私以为,练习归练习,学习归学习,但不能只会做一个传道者,
迷信工具,迷信顶层,而没有透彻的基础认识。
工具看了手册谁都会用,为什么用,怎么用,好不好则更加重要。
就像是学习语言或是诊断学,迷信书本只知所以然是万万不可的。
——只会利用工具的人,终究会被工具抛弃。
回到问题上来。
N皇后问题中,穷举法的复杂度为(n!),
但若是采用和某些逻辑题一样的算法,则可以大大简化代码。
首先,国际象棋的后拥有两种攻击方式:
好似城堡的十字攻击以及骑士的对角攻击,攻击范围无限制:
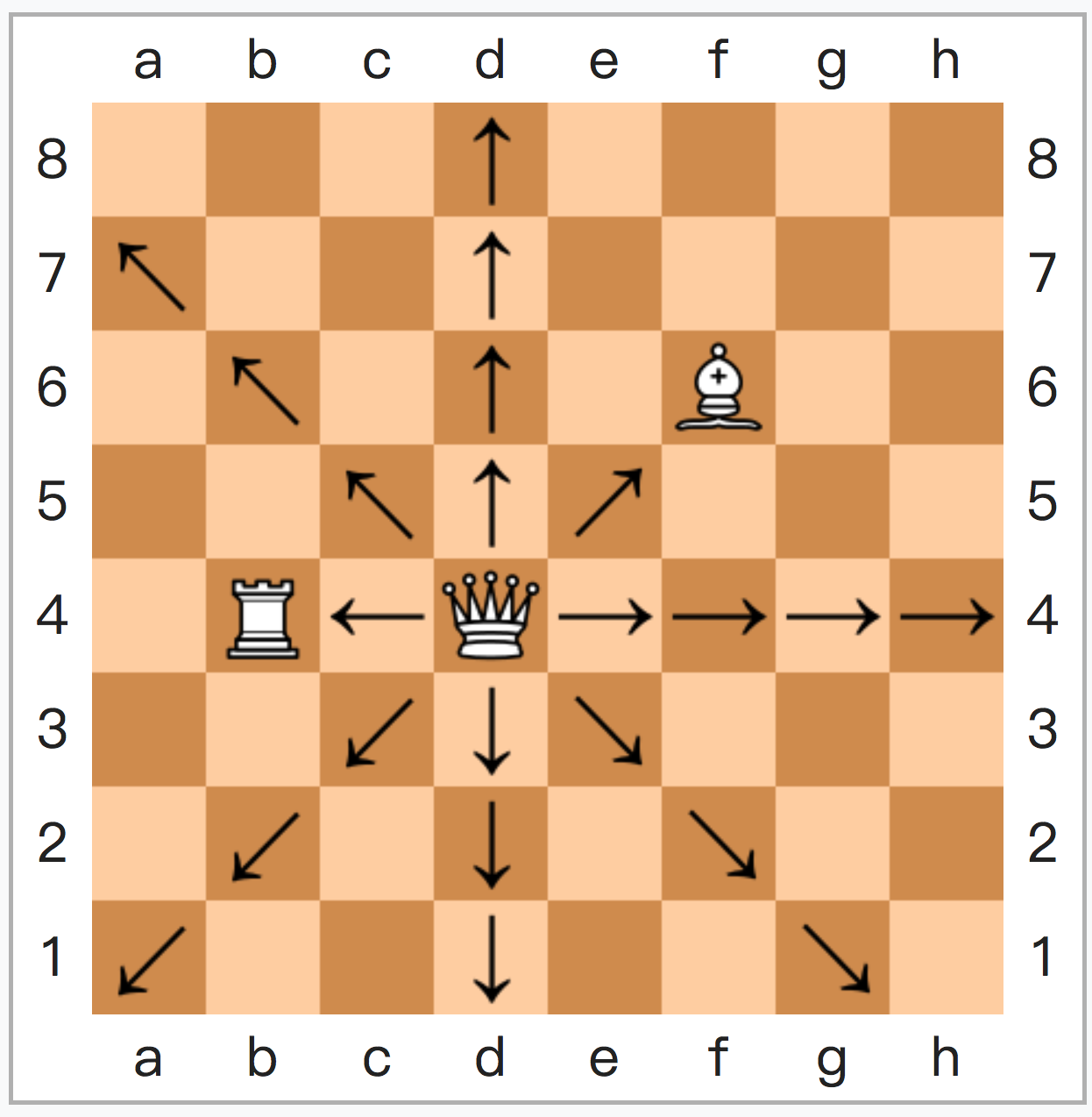
从而得出两个预结论——
1 N皇后于NxN棋盘上,若老死不相往来,则绝不在同一行列。
2 攻击范围有重叠时,绝非边与边重叠,只可相交,且相交仅会出现一次。
于是便可以将棋盘格子赋予是否安全的属性,1为受到攻击位置,0安全。
从第一条边向第八条边推进,标注所有可能的攻击位置,发现0则置子,
发现一个以上的安全位置,则从一个方向起下子,深度优先遍历。
于是使用位运算,将n~1横列化为n个二进制数,指定0位安全;
由预结论1,不考虑所下子横行上的攻击(下子后必然全为1);
由预结论1,copy下子所在竖列的状态至下一行;
利用位移运算符定义两种对角攻击模式。
以上图第4横行为例,下子状态标注为 0001 0000
(计算第5横行时,下子状态保留为 0001 0000,
攻击范围则将下子状态左移/右移一位,
分别是 0010 0000 和 0000 1000。
将三个状态列取或运算,则结果中的0位为安全位置。
于是——
#include <iostream>
// total:记录解;finishline:确认的行
int total = 0, finishline = 1;
// row:竖直攻击; ls:斜杠攻击; rs:反斜杠攻击
void trying(long row, long ls, long rs)
{
if (row != finishline) // 开始新行
{
long position = finishline & ~(row | ls | rs);
while(position) // 若行间无位可放...
{
long pointline = position & -position;
position -= pointline;
trying(row + pointline, (ls + pointline) << 1, (rs + pointline) >> 1);
}
}
else
{
total++;
}
}
using namespace std;
int main(int argc, char *argv[]) {
int grid = 8; // 修改grid的话,1~31皇后都能解w
finishline = (finishline << grid) - 1;
trying(0, 0, 0);
cout << total << endl;
return 0;
}
事就这么成了。
回到最早的知乎问题上去。我真的不明白为什么要限制行数,
而不是限制时间和内存,
但也因为这个问题看似哗众取宠,
便在想是不是某种形式的软广告。
不过最有意思的事情是问题下面百花齐放的代码。
有人简化变量名到一个字符,有人省略头文件,
有人把所有的东西挤成一行,自然注释都没有。
不用说美感,就连维护都是问题。
自己都看不懂了,就为了10行,图啥?
可谓是为完成任务而完成任务了的哗众取宠了。
还有人直接就import <8queens>,
抑或是贬损除了暴力枚举之外的其他算法,
真的是不知道什么逻辑了。
学习计算机科学到现在,傻喵越来越觉得,
好多东西都是如此相通的——
会用工具却拘泥于工具的人;
认为掌握工具便算精通的人;
知道规则便想创造规则的人;
末法心态的,实用主义的人。
希望我不会变成他们那样。。。
更愿意从数学汇编一步步学起,
就像当年从解剖学一步步学起,
就像当年从桥本文法开始学起,
就像当年从吹长音一步步学起,
这样,我想算是专业的负责吧。
不管。总之先把题答了——
#include <iostream>
int total = 0, finishline = 1;
void trying(long row, long ls, long rs){
if (row != finishline) { long position = finishline & ~(row | ls | rs);
while(position) { long pointline = position & -position; position -= pointline; trying(row + pointline, (ls + pointline) << 1, (rs + pointline) >> 1); }} else {total++;}}
using namespace std;
int main(int argc, char *argv[]) {
int grid = 8; // 修改grid的话,1~31皇后都能解w
finishline = (finishline << grid) - 1; trying(0, 0, 0); cout << total << endl;
return 0;}
嗯。能看得懂,10行也就差不多这样了。
不过,如果八皇后问题真的会在项目里用到,
我则绝不会使用上面的所有程序,而会——
// 此处需使用八皇后算法,但忽略计算过程,仅使用答案节省时间。
// 八皇后解枚举数据头在******
void 8queensAnswers (0, 0, 0, 0)
//在里面做一个调用92个答案的接口,传参出去给大结构体
//保存各个答案类似于[91, 0, 4, 7, 5, 2, 6, 1, 3]这样
//或者n皇后的话[0,1][1,0][2,0][3,2][4,10][5,40]...这样
复杂度为1或是常数n,为啥不用?多好。
至于说怎么显示N皇后问题的解的话w
手动艾特@CocoaOikawa~
N皇后问题——记录下那些老死不相往来的N个女人的位置吧
以上ヾ(๑╹◡╹)ノ”



 (八皇后问题的其中一个解)
(八皇后问题的其中一个解)

