——那是因为我搞不清形式语言和非形式语言 (v0.02)
自去年开始,自觉之前大学所学的基础学科不够用,想要补补课的我,从 cocoa 留下的那一本离散数学的笔记出发,被 b1 带着钻到计算理论,而后跑到了数学的世界里。作为一个常游泳但嫌水冷都要磨叽半天的我,跳进非舒适区的感觉自然不那么好,于是希望有类似经历的人不再和我一样辛苦得很可怜,就不断地在这边开坑;加之,我想借这个地方纪念我所学的和给我带来帮助的人,我觉得与其期待论文致谢把大家的名字说出来,不如时时用这种方式感谢那些在我平凡日子里嵌进一颗颗宝石的人,所以如果在看这些博客的你有想和我分享的东西,也请不吝赐教哦/
那么 进入正题——
我们大学阶段所看的数学教材,大体是会如此组织:
先是公理,然后是定理,然后可能有一些定义啊、推论、引理(为了证明什么新的东西出来)以及夹杂其间的例子以及证明。然后是习题啊啥啥的;有些实用性强的教材,比如我先前本科经济学的教材,则不注重理论和证明,东西能用就好(何况在高频交易的世界里学了微积分也用不上emmmm)
这样学习的好处是可以不纠结基础理论,也可以说是可以高屋建瓴:不用在数学的大厦里往地基推进。很多人(比如我)能用数学解决问题,但是什么数理逻辑啊模型论啊公理化集合论啊递归论(可计算性理论)还有证明论啥啥的都没听过,也没耽误做医学统计搞经济模型或者机器学习。
但是对于跨学科的人来讲,如果有基础科学的加持,便可以不用在新领域里只得做一个解题能手,因为你可以从更底层去思考问题,这是科班出身的人会有但往往不扎实的能力。
在滚动更新的时候,没必要在学一份“经济数学”再来一份“医学数学”再来一份“计算机数学”的时候,把所有的共通线重刷好几遍——经济数学、医学数学、计算机数学应该像是DLC那样,装载在数学范式的本体上;而对于像我这样先前有安装实用数学(我姑且这么叫)的人,我给自己的建议,还是要把数学的部分滚动更新一下的。
那我来说说为什么我读不懂数学书吧。
简单来讲,最重要的一个事情是:数学语言和我们的日常语言很不一样
这里要讲一个概念叫【元数学】。元数学是指一种“将数学视为人类意识和文化客体的科学思维或知识”,它使用数学技术来解决数学问题,是研究数学和数学哲学的数学。
我可能记不太清了,b1 有一次和我说,主要用非数学语言,比如汉语描述数学的过程,是元数学研究;多讲一句,这算是元数学的三道门中的第一道:
1 将非形式化的理论“形式化”,得到
2 (一般的)形式体系和特殊的形式体系——对象理论,而后
3 借用元理论,描述并研究形式体系 最后使你到到达了数学的世界
在这个过程中,元理论是会使用很多寻常语言的:比如你看哥德尔不完备定理的全文,在他的论述前有 20 多页的前言,全是用非数学语言叙述;论证的过程中,也不像你我看到的数学书那样充满符号。
但是一旦离开了数学的天空之城——元数学的范畴,我们便来到了地上的城——数学。至于说为什么元数学不是数学,可以思考一下理查兹悖论。这个城市和元数学不同,是建立在以“公理化集合论”为代表的“数理逻辑”上的;或者说,当今数学世界的范式,是数理逻辑。这个世界里充满了形式语言,它是用精确的数学或机器可以处理的公式定义的语言;在这里,偶尔出现的非形式化语言只能给人家做个点缀(这时候我们称这种形式化非形式化掺杂的语言为‘半形式化语言’)。
形式语言和非形式语言虽然都有语言学上的“语法”和“语义”,但它们行同陌路。
从最小的符号的定义上都截然不同。这便是为什么我看数学系的教材往往是似懂非懂的。
你看,我们定义非形式语言为“一套复合交流系统”;定义形式语言为“一个字母表上的某个有限长字符串的集合”。真的你瞅瞅,这俩东西咋看咋不是一家的。
所以说了这么多,搞不明白形式语言和非形式语言的区别,拿着应用数学的知识和非形式化语言的逻辑,想看懂数学的教材,对于我们这些外行人来讲一定是相当困难的事情。想要搞懂数学书上是什么内容,我认为要从熟悉形式语言和符号入手;若是懂一些公理化集合论和数理逻辑,那就最好了。
那么最后问一个问题,为什么形式语言都写在数学书里呢?
要回答这个问题,我想让你先想象自己是像欧拉那样的,每天脑子里都会蹦出改变世界的新想法的天才数学家。别谦虚,想就是了w
你的脑子里有新的点子:于你而言,你是有一套天才的证明方法的;事实上,我相信每个数学家都有自己特色的核心处理法,直觉也算。但是你的证明方法别人不一定能听懂,你的灵感源泉无法向别人解释,更要命的是你无法百分百证明自己的点子是正确的,因为你的核心处理法不一定百试百灵。那怎么办?
为了能够跟你眼中够不上你的大多数人,或是和你有不同研究个性的同侪们解释你的点子,你首先要尝试把它翻译成人人都能精准理解的某种语言,然后再给对方。不论是解释、证明还是争辩,你都要用这种精准的、没有歧义的语言来转换你的点子、你的想法;这样你便保证了你思想的果实可以完整地传递给他人。当然他人怎么把这种中间语言转换成他的理解那就不是我们要管的事儿了。——精准地传递信息,这就是形式语言的意义。这种经过公认考验和提炼的精准语言的格式,我们称为数学范式。
有了形式语言的另一个好处是,我们可以划定处理问题的边界,或者不确切地说,“我们所表述所研究的数学理论”是什么。确切来讲则是:相对于元数学,数学是什么。我们还是假设你是一个为你所在的某个领域做出贡献的数学家,你希望你所做的描述不只符合某种特殊情况,而是尽可能地具有普适性,可以用在各种具有某些共同性质的东西上。我们便把这些共同性质抽提成为一个集合的性质/运算,把那些具有共同性质的东西抽提为集合中的元素,这种带有元素还带有运算的东西,我们可以称之为“空间”;这种公论承认、无需证明的共同性质,我们叫它们“公理”。比如构造线性空间的 8 条公理:
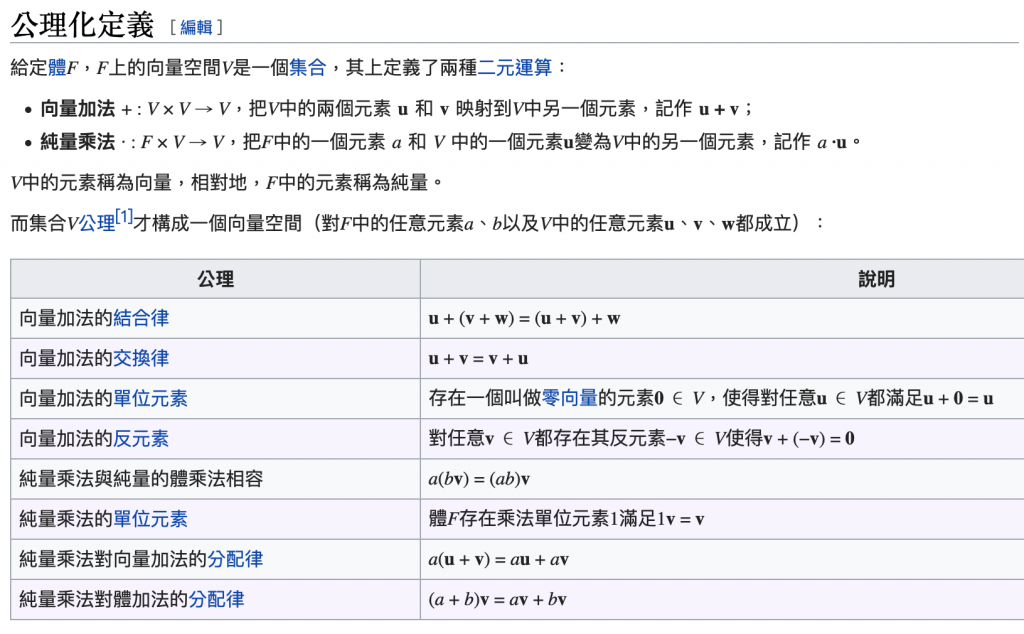
只要你想让你的理论和概念在这个空间里适用,那么你一定要满足这 8 条公理;如果别的数学家或者你的学生搞出了新的想法,你也可以用“这些想法是否满足这 8 条公理”来验证。把公理作为集合的元素后,我们便有了“公理系统”;把公理和它们导出的所有定理总括起来,我们把它称为“数学理论”。数学理论的范围,可以说便是相对于元数学的数学世界了。我没有使用“范畴”这个词,是因为不想让你重写范畴论里的范畴定义w
形式/半形式语言写就的公理,和你在书上看到的那些形式化/半形式化语言一样,它们不是自然法则,它们是一座座桥,连接着你、你的同侪和那些伟大的数学家。为了这座桥的平整牢靠,我们使用“抽象化”来处理这座桥的模型,便成就了它极简抽象、晦涩难懂的风格。你的目的和困难,在于把桥的模型了然于胸;至于之后你如何装点你心里的桥,那便是你的事情了。
最后,形式语言、非形式语言、公理化集合论、数理逻辑等等的定义本身,维基百科说得肯定比我好,那样的知识也俯拾即是,我便不再赘言了w
下一次,我想讲一讲“为什么我看不懂数学符号”
或 “为什么我看不懂数学证明”

